Solving a Maze

Solving mazes seems like a really good opportunity to continue exploring using graph-processing techniques to solve interesting problems.

from pathlib import Path

import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import networkx as nx

Generating Mazes

We could probably create mazes using Python, but that’s outside the scope of this tutorial. Instead, we’ll use this amazing resource:

https://www.allkidsnetwork.com/mazes/maze-generator

This site requires you to create an account and login, so I created a maze and downloaded it locally.

maze_file_path = Path("../res/maze.png")
assert maze_file_path.exists()

Loading a Maze as an Image

We’ll load mazes as images, then perform our computations on the image.

maze = mpimg.imread(maze_file_path)
plt.imshow(maze)
plt.show()

Solving the Maze with a Graph

As usual, we’ll use networkx because it’s awesome!

Here’s the game plan:

1. Create a graph using the image

2. Initially, all pixels will be connected to their neighbors

3. We’ll remove any connections (edges) for pixels that are not possible paths

• White pixels represent possible paths

• Any pixels other than white represents a wall

• Pixels outside the maze are not possible paths

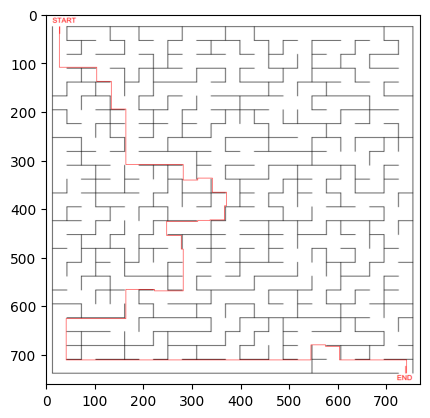
4. Find the shortest path from beginning to end

5. Overlay the path onto our maze image and visualize it

nrows, ncols, _ = maze.shape

graph = nx.grid_2d_graph(nrows, ncols)

edges_to_remove = []

top_of_maze = 25
bottom_of_maze = nrows - 22
left_of_maze = 13
right_of_maze = ncols - 14

for node in graph.nodes:
    row, col = node
    is_not_path = (maze[row, col, 0:3] != 1).all()
    is_outside_of_maze = any(
        [
            row < top_of_maze,
            row > bottom_of_maze,
            col < left_of_maze,
            col > right_of_maze,
        ]
    )
    if is_not_path or is_outside_of_maze:
        edges_to_remove.extend((node, n) for n in graph.neighbors(node))

graph.remove_edges_from([edge for edge in edges_to_remove])

start = (top_of_maze + 1, left_of_maze + 14)
end = (bottom_of_maze - 1, right_of_maze - 14)

path = nx.shortest_path(graph, start, end)

for step in path:
    row, col = step
    maze[row, col] = [1, 0, 0, 1]
plt.imshow(maze)
plt.show()

Conclusion

There are obvious improvements that we can make, but this was just for fun.

I hope you enjoyed seeing how to solve mazes with Python and networkx!